16. A rajzon lévő többszintű NAND hálózatot kell elemeznie. Írja fel az egyes szintek logikai függvényeit és a kimeneti függvényt! A kimeneti függvényben a De-Morgan-azonosságot alkalmazva mutassa meg az egyes szinteken megvalósuló logikai függvényeket! Felkészülése és felelete során használja az alábbi információkat!

1, Kombinációs hálózatok:

Számos digitális elektronikai alkalmazás esetén olyan áramkörre van szükség, amely számos bemenetet és kimenetet tartalmaz, valamint a pillanatnyi bemenetek egyértelműen meghatározzák az aktuális kimenetet. Ezeket az áramköröket kombinációs hálózatoknak nevezik. Nem minden áramkör rendelkezik ezzel a tulajdonsággal. Például olyan áramkörök, amelyek memóriaelemeket is tartalmaznak, olyan kimenetet is adhatnak, amik a bemeneti változókon kívül a memória tartalmától is függnek, ezeket szekvenciális hálózatoknak nevezzük.

PL: - multiplexerek, dekóderek

A kombinációs hálózat nem időfüggő, azaz a kimenetek értéke mindig a bemenetek aktuális értékétől függ csak.

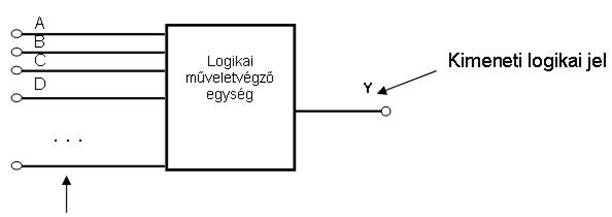
A bemeneteket független változóknak nevezzük, és az angol ABC nagybetűivel jelöljük. A kimeneteket függő változóknak hívjuk, és F-fel, Y-al, vagy Q-val jelöljük. Több kimenet esetén a kimeneteket alsó indexxel látjuk el, amit 0-tól kezdve számozunk.

2, A NAND függvény, igazságtáblázat. A NAND kapu:

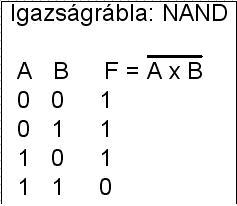
NEM-ÉS: NOT-AND = NAND

- ÉS kapcsolat ellentettje

- Több-bemenetű logikai kapu, amelynek kimenetén csak akkor jelenik meg 0 (L)szint, ha az összes bemenetén 1-es, (H) szint van.

-Jele: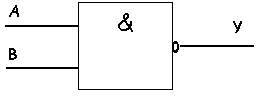

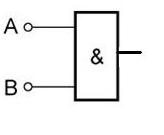
3, AND függvény, igazság táblázata:

ÉS=AND

-A kimenet értéke csak akkor „1” ha az összes bemenet értéke „1”.

-Jele: -Igazságtábla:

4, De-Morgan azonosság:

- Az azonosság Augustus de Morgan angol matematikusról kapta a nevét.

- Az ÉS kapcsolat és a VAGY kapcsolat közötti átalakításra lehet használni.

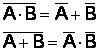
1, A változók „ÉS” kapcsolatának negáltja (NAND) egyenlő a változók negáltjainak „VAGY” kapcsolatával.

2, A változók „VAGY” kapcsolatának negáltja (NOR) egyenlő a változók negáltjainak az „ÉS” kapcsolatával.

5, Logikai algebra szabályai:

Az analóg rendszer ki- és bemenetei közötti kapcsolatot folytonos függvények adják meg. (gondoljunk arra, hogy egy analóg Volt-mérő kapcsaira csatolt feszültség nagysága miképp befolyásolja a mutató kitérését). A kombinációs hálózatok ki- és bemenetei közötti összefüggések logikai függvényekkel írhatók fel. Ehhez a matematikai alapot a Boole-algebra adja.

A Boole-algebra a kétértékű jelekkel végzett logikai műveletek algebrai leírását teszi lehetővé. Szabályai:

§ Bármely változó lehetséges értékei: 0 vagy 1.

§ Elvégezhető műveletek:

Logikai szorzás (konjunkció), ÉS kapcsolat:

0 ^.0=0

0 ^.1=0

1 ^.0=0  

1 ^.1=1

Logikai összeadás (diszjunkció), VAGY kapcsolat:

0+0=0 -Felcserélhetőség:

0+1=1 A+B=B+A

1+0=1 -Csoportosíthatóság

1+1=1 A+(B+C) = (A+B)+C

-Logikai tagadás (negáció): -Kiemelhetőség:

A×B+A×C = A× (B+C)

-Alaptételek, azonosságok:

6, A többszintű kombinációs hálózat elemzése:

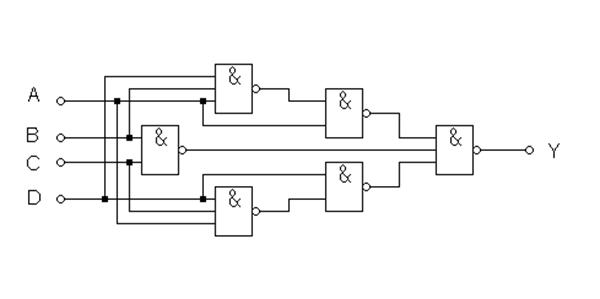
A De-Morgan azonosság felhasználásával:

Ismét a De-Morgan azonosságot használva:

A zárójelek felbontása után:

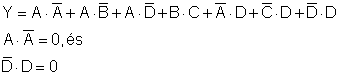
Ezért: